Python toolset for statistical comparison of machine learning models and human readers

Introduction

The most common statistical methods for comparing machine learning models and human readers are p-value and confidence interval. Although receiving some criticism recently, p-value and confidence interval give more insight into results than a raw performance measure, if interpreted correctly, and are required by many journals.

This post shows an example python code utilizing bootstrapping for computing confidence intervals and p-values comparing machine learning models and human readers.

I will not discuss what p-value does or does not mean, what is the right threshold for statistical significance, or how to properly interpret it. Here are some resources that dive deeper into this topic:

Wasserstein, R.L. and Lazar, N.A., 2016. The ASA’s statement on p-values: context, process, and purpose. The American Statistician, 70(2), pp.129-133.
Baker, M., 2016. Statisticians issue warning over misuse of p-values. Nature News, 531(7593), p.151.
Altman, N. and Krzywinski, M., 2016. Points of significance: p-values and the search for significance.
Benjamin, D.J., Berger, J.O., Johannesson, M., Nosek, B.A., Wagenmakers, E.J., Berk, R., Bollen, K.A., Brembs, B., Brown, L., Camerer, C. and Cesarini, D., 2018. Redefine statistical significance. Nature Human Behaviour, 2(1), p.6.
McShane, B.B., Gal, D., Gelman, A., Robert, C. and Tackett, J.L., 2019. Abandon statistical significance. The American Statistician, 73(sup1), pp.235-245.

Simple statistical toolset for machine learning

I published a GitHub repository ml-stat-util containing a set of simple functions written in Python for computing p-values and confidence intervals using bootstrapping. I will show how to use it in different common use cases.

A jupyter notebook with all use cases described below is available on GitHub.

Use case #1

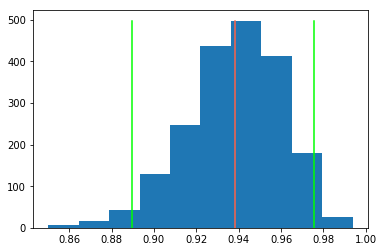
Compute AUC with 95% confidence interval for a single model.

from sklearn.metrics import roc_auc_score
import stat_util

score, ci_lower, ci_upper, scores = stat_util.score_ci(
    y_true, y_pred, score_fun=roc_auc_score
)

To get an idea of what happened, we can plot a histogram of bootstrapped scores.

import matplotlib.pyplot as plt

bins = plt.hist(scores)
plt.plot([score, score], [0, np.max(bins[0])], color="tomato")
plt.plot([ci_lower, ci_lower], [0, np.max(bins[0])], color="lime")
plt.plot([ci_upper, ci_upper], [0, np.max(bins[0])], color="lime")

Histogram CI

Use case #2

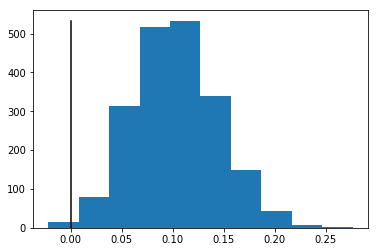
Compare two models by computing p-value for a difference in their performance measured with AUC.

from sklearn.metrics import roc_auc_score
import matplotlib.pyplot as plt
import stat_util

p, z = stat_util.pvalue(y_true, y_pred1, y_pred2, score_fun=roc_auc_score)
bins = plt.hist(z)
plt.plot([0, 0], [0, np.max(bins[0])], color="black")

Histogram p-value

Use case #3

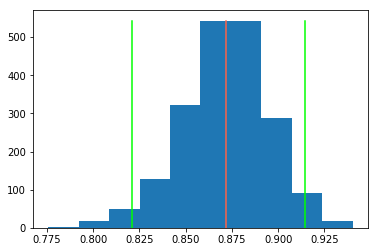
Compute mean AUC with 95% confidence interval for a set of readers/models.

import numpy as np
from sklearn.metrics import roc_auc_score
import matplotlib.pyplot as plt
import stat_util

mean_score, ci_lower, ci_upper, scores = stat_util.score_stat_ci(
    y_true, y_pred_readers, score_fun=roc_auc_score, stat_fun=np.mean
)
bins = plt.hist(scores)
plt.plot([mean_score, mean_score], [0, np.max(bins[0])], color="tomato")
plt.plot([ci_lower, ci_lower], [0, np.max(bins[0])], color="lime")
plt.plot([ci_upper, ci_upper], [0, np.max(bins[0])], color="lime")

Histogram CI mean

Use case #4

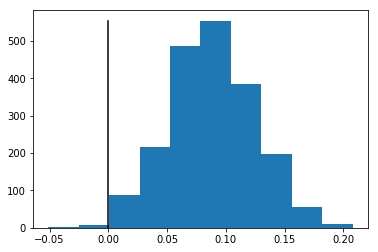
Compare a single model to a set of readers by computing p-value for a difference in their performance measured with AUC.

import numpy as np
from sklearn.metrics import roc_auc_score
import matplotlib.pyplot as plt
import stat_util

p, z = stat_util.pvalue_stat(
    y_true, y_pred, y_pred_readers, score_fun=roc_auc_score, stat_fun=np.mean
)
bins = plt.hist(z)
plt.plot([0, 0], [0, np.max(bins[0])], color="black")